A continuacion mas ejercios de combinacion lineal, depedencia e independencia lineal y tambien algunos video
1. Determinar si el conjunto de vectores v1 = (1, -2, 3) v2 = (5, 6, -1)
v3 = (6, 4, 2) son linealmente dependientes y reporte la solucion.
Para saber si son lineales se debe generar la siguiente ecuacion:
k1v1 + k2v2 + k3v3 = vector 0
Para resolver esto se debe plantear los vectores como si fueran las columnas de un sistema de ecuaciones de 3x3 siendo las incognitas k1,k2 y k3
2R + R1
1........5........6.............[ 0 ]
-2.......6........4.............[ 0 ]
3.......-1........2.............[ 0 ]
R2 + R3
1........5........6.............[ 0 ]
0........16.......16............[ 0 ]
0.......-16......-16............[ 0 ]
1/16R2
1........5........6.............[ 0 ]
0.......16.......16.............[ 0 ]
0........0........0.............[ 0 ]
-5R2 + R1
1........5........6.............[ 0 ]
0........1........1.............[ 0 ]
0........0........0.............[ 0 ]
1........0........1.............[ 0 ]
0........1........1.............[ 0 ]
0........0........0.............[ 0 ]
k1 + k3 = 0
k1 = -k3
k2 + k3 = 0
k2 = -k3
k3 = k3
k3 = k3
k1 [ -1 ]
k2 [ -1 ]
k3 [ 1 ]
SOLUCION: los vectores entre si son linealmente dependientes
viernes, 26 de marzo de 2010
ESPACIO VECTORIAL CON PRODUCTO INTERNO Y SUS PROPIEDADES
Sean X = ( x 1, x 2, ..., x n ), Y = ( y 1, y 2, ..., y n ) dos vectores arbitrarios de
Rn. Definimos el producto interno de X e Y así:
X, Y = å
i=1
n
x i y i. (1.2.1)
Las propiedades de (1.2.1) son:
1. X, Y = Y, X .
2. X + Z, Y = X, Y + Z, Y .
3. lX, Y = l X, Y .
Las propiedades 2. y 3. nos dicen que el producto interno es lineal en la primera variable. Por la
propiedad 1. concluimos que también lo es en la segunda variable.
Existen en la literatura matemática otras notaciones para el producto interno, por ejemplo: X.Y y se le
conoce con el nombre de producto punto. Otra notación, bastante aparatosa, es X|Y , que
aparece frecuentemente en los libros de Física.
Con esl uso del producto interno introducimos uno de los conceptos más notables en matemáticas: la
norma de un vector.
Definición (1.2.2): Sea X = ( x 1, x 2, ..., x n ) Î Rn, definimos la norma de X así:
X = X, X = å
i=1
n
x i
X = X, X = å
i=1
n
La longitud (norma) de un vector de Rn es V = (v1, v2, ..., vn ) esta dada por:
________________
||V|| =" v12 + v22 + ... + vn2 esta no puede ser negativa si el vector v = 1 este se llama vector unitario dos vectores U y V en Rn son paralelos si al vector V es múltiplo del vector U, es decir, si U = cV si c > 0 los vectores van a la misma dirección y si c < 0 van en dirección opuesta, la longitud de un múltiplo escalar se ve por la formula || cV || = | c | || V || donde | c | es el valor absoluto de c y c es un escalar.
El vector unitario de V es si V " 0 entonces U = V / ||V|| es de longitud uno y tiene la misma dirección de U+V se llama vector unitario en dirección de V este proceso se llama normalización del vector V.
La distancia entre dos puntos se llama normalización del vector V.
___________________
d =" (u1 - v1 )2+ (u2 - v2 )2 y la distancia entre dos vectores en R2 se encuentra .
___________________
d(U,V) = || U - V || =" (u1 - v1 )2+ (u2 - v2 )2 donde U = (u1 - u2 ) y V = (v1 - v2 ).
Las propiedades que cumple la distancia son:
d( U , V ) " 0.
d( U , V ) = 0 si solo si U = V.
d( U , V ) = d( V , U ).
Para encontrar el ángulo entre dos vectores distintos de cero usamos la formula:
Cos = (u1v1 + u2v2) / ||U|| ||V|| donde U = ( u1, u2 ) y V = ( v1 , v2 ) y donde u1v1 + u2v2 se denota como producto punto de dos vectores. El producto punto para Rn se denota U % V = u1v1 + u2v2 + ... + unvn las propiedades que cumple son :
U % V = V % U
U % (V + W) = U % V + U % W
c ( U % V ) = cU % V = U % cV
V % V " ||V|| 2
V % V " 0 y V % V = 0 si solo si V = 0
Donde c es un escalar y que U, V, W son vectores cualesquiera en Rn.
Desigualdad de gauchy - schawarz:
La desigualdad de Gauchy - Schwarz dice que | U % V | " || U || || V || don de | U % V | es valor absoluto de U % V donde U y V son vectores viendo esta desigualdad podemos definir el ángulo entre dos vectores en Rn así : Cos = (U % V ) / (||U|| ||V||) esta formula no define ángulos entre dos vectores, si U % V = 0 se dice que los ángulos son ortogonales.
La desigualdad del triangulo:
Dice si U y V son vectores entonces || U + V || " || U || + || V ||.
El teorema de Pitágoras:
Este dice si U y V son vectores entonces || U + V ||2 = || U || 2 + || V || 2 solo para vectores ortogonales.
Un producto punto es un producto interno Euclidiano esto es un producto interno que se puede definir en R2. para poder diferenciar el producto interior de otros posibles productos internos lo escribiremos esto será el producto general para el espacio vectorial V.
Para solucionar un producto interno se procede igual que al definir un espacio vectorial en el acho de que debe cumplir con varios axiomas para poder calificar como producto interno estos axiomas son:
Siendo U, V, W vectores en V y c cualquier escalar:
=
= + o = +
c =
" 0 y = 0 si solo si v = 0
= = 0
Para definir la norma, distancia, ángulo de dos vectores que tenga producto interno:
siendo U, V vectores en V:
______
norma = ||U|| = "
distancia entre U, V = d= || U - V ||
ángulo entre vectores U, V diferentes de 0 cos = / ( ||U|| ||V|| ) donde 0 " " .
Dos vectores con producto interno son ortogonales si = 0. El vector unitario de un vector con producto interno || U || = 1 el vector unitario en dirección de V donde U = V / || V || donde V " 0. Para ver si U y V son vectores en el espacio con producto interno deben cumplir con las propiedades de norma:
|| U || " 0.
|| U || = 0 si solo si U = 0.
|| cU || = | c | || U ||.
Y las propiedades de la distancia antes ya mencionadas.
Además cumplen con la desigualdad de Gauchy - Schawarz, desigualdad del triangulo y el teorema de Pitágoras antes yya explicadas.
Proyecciones ortogonales en espacios con producto interno:
Si U y V son vectores en el plano y V es diferente de 0 entonces este se puede proyectar ortogonalmente a U y se denota como
ProyV U = [ ( U%V ) / ( V%V ) ]V
proyU V = [ ( U%V ) / ( U%U ) ]U donde U%V y V%V son el producto punto o producto interno Euclidiano.
Para en el espacio la proyección se denota como proyv U = [ / ]V , proyv U = [ / ]U.
La proyección ortogonal y distancia:
Siendo U y V dos vectores en el espacio V con producto interno y V " 0. Entonces la distancia d ( U, proyv ) < d ( U, cV ) donde c " / .
Definición de conjuntos ortonormales y conjuntos ortogonales:
En un conjunto de vectores S de el espacio vectorial V es producto interno es ortogonal si cada vector de y seria espacio ortonormal si cada vector S es unitario.
Es ortonormal si < vi, vj > = 0 i " j y || vj || = 1 donde i = 1, 2, 3, ..., n y es ortonormal si < vi, vj > = 0 i " j donde vi, vj pertenecen al conjunto s = { v1, v2, ..., vn }
Un conjunto ortogonal es linealmente independiente si s es un conjunto de vectores diferentes de cero y que pertenecen al espacio v con producto interno.
Proceso para ortonormalizar de Gram - Schmidt:
Ver si la base tiene producto interno (como ya lo vimos).
Convertir la base a una base ortogonal.
Sea B = { v1, v2, ..., vn }
w1 = v1
w2 = v2 - proyw1 v2
wn = vn - proyw1 v3 - … - proyw(n-1) vn
B' = { w1, w2, ..., wn }
y para ortonormalizar ui = wi / ||wi|| donde I = 1, 2, ..., n.
Donde B'' = { u1, u2, ..., un } es un abase ortonormal.
Aplicación de los espacios con producto interno:
Producto cruz de dos vectores en el espacio:
Donde U = (u1, u2, ..., un )
V = (v1, v2, ..., vn )
U x V =
por el método de cofactores = i + j + k .
las propiedades del producto cruz:
U x V = V x U
c ( U x V ) = c U x V = U x c V
U x U = 0
U x ( V + W ) = ( U x V ) + ( U x W )
U x 0 = 0 x U
U ( V x W ) = ( U x V ) W
U x V son paralelos si U x V = 0.
Aproximación por mínimos cuadrados:
Siendo f y g dos funciones en x y funciones continuas en un intervalo finito [ a, b ] entonces.
I = 2 dx siendo I = 0 si ( f - g ) ! 0 esto se puede representar como :
= 2 dx siendo I = 2 dx = = || f - g || 2 esto significa que es equivalente minimizar || f - g || 2 y || f - g ||.
La aproximación de minimos cuadrados esta dada por:
g = w1 +w2 + ... + wn siendo w1 = w1 donde b = {w1, w2, w3,}
Rn. Definimos el producto interno de X e Y así:
X, Y = å
i=1
n
x i y i. (1.2.1)
Las propiedades de (1.2.1) son:
1. X, Y = Y, X .
2. X + Z, Y = X, Y + Z, Y .
3. lX, Y = l X, Y .
Las propiedades 2. y 3. nos dicen que el producto interno es lineal en la primera variable. Por la
propiedad 1. concluimos que también lo es en la segunda variable.
Existen en la literatura matemática otras notaciones para el producto interno, por ejemplo: X.Y y se le
conoce con el nombre de producto punto. Otra notación, bastante aparatosa, es X|Y , que
aparece frecuentemente en los libros de Física.
Con esl uso del producto interno introducimos uno de los conceptos más notables en matemáticas: la
norma de un vector.
Definición (1.2.2): Sea X = ( x 1, x 2, ..., x n ) Î Rn, definimos la norma de X así:
X = X, X = å
i=1
n
x i
X = X, X = å
i=1
n
La longitud (norma) de un vector de Rn es V = (v1, v2, ..., vn ) esta dada por:
________________
||V|| =" v12 + v22 + ... + vn2 esta no puede ser negativa si el vector v = 1 este se llama vector unitario dos vectores U y V en Rn son paralelos si al vector V es múltiplo del vector U, es decir, si U = cV si c > 0 los vectores van a la misma dirección y si c < 0 van en dirección opuesta, la longitud de un múltiplo escalar se ve por la formula || cV || = | c | || V || donde | c | es el valor absoluto de c y c es un escalar.
El vector unitario de V es si V " 0 entonces U = V / ||V|| es de longitud uno y tiene la misma dirección de U+V se llama vector unitario en dirección de V este proceso se llama normalización del vector V.
La distancia entre dos puntos se llama normalización del vector V.
___________________
d =" (u1 - v1 )2+ (u2 - v2 )2 y la distancia entre dos vectores en R2 se encuentra .
___________________
d(U,V) = || U - V || =" (u1 - v1 )2+ (u2 - v2 )2 donde U = (u1 - u2 ) y V = (v1 - v2 ).
Las propiedades que cumple la distancia son:
d( U , V ) " 0.
d( U , V ) = 0 si solo si U = V.
d( U , V ) = d( V , U ).
Para encontrar el ángulo entre dos vectores distintos de cero usamos la formula:
Cos = (u1v1 + u2v2) / ||U|| ||V|| donde U = ( u1, u2 ) y V = ( v1 , v2 ) y donde u1v1 + u2v2 se denota como producto punto de dos vectores. El producto punto para Rn se denota U % V = u1v1 + u2v2 + ... + unvn las propiedades que cumple son :
U % V = V % U
U % (V + W) = U % V + U % W
c ( U % V ) = cU % V = U % cV
V % V " ||V|| 2
V % V " 0 y V % V = 0 si solo si V = 0
Donde c es un escalar y que U, V, W son vectores cualesquiera en Rn.
Desigualdad de gauchy - schawarz:
La desigualdad de Gauchy - Schwarz dice que | U % V | " || U || || V || don de | U % V | es valor absoluto de U % V donde U y V son vectores viendo esta desigualdad podemos definir el ángulo entre dos vectores en Rn así : Cos = (U % V ) / (||U|| ||V||) esta formula no define ángulos entre dos vectores, si U % V = 0 se dice que los ángulos son ortogonales.
La desigualdad del triangulo:
Dice si U y V son vectores entonces || U + V || " || U || + || V ||.
El teorema de Pitágoras:
Este dice si U y V son vectores entonces || U + V ||2 = || U || 2 + || V || 2 solo para vectores ortogonales.
Un producto punto es un producto interno Euclidiano esto es un producto interno que se puede definir en R2. para poder diferenciar el producto interior de otros posibles productos internos lo escribiremos esto será el producto general para el espacio vectorial V.
Para solucionar un producto interno se procede igual que al definir un espacio vectorial en el acho de que debe cumplir con varios axiomas para poder calificar como producto interno estos axiomas son:
Siendo U, V, W vectores en V y c cualquier escalar:
=
= + o = +
c =
" 0 y = 0 si solo si v = 0
= = 0
Para definir la norma, distancia, ángulo de dos vectores que tenga producto interno:
siendo U, V vectores en V:
______
norma = ||U|| = "
distancia entre U, V = d= || U - V ||
ángulo entre vectores U, V diferentes de 0 cos = / ( ||U|| ||V|| ) donde 0 " " .
Dos vectores con producto interno son ortogonales si = 0. El vector unitario de un vector con producto interno || U || = 1 el vector unitario en dirección de V donde U = V / || V || donde V " 0. Para ver si U y V son vectores en el espacio con producto interno deben cumplir con las propiedades de norma:
|| U || " 0.
|| U || = 0 si solo si U = 0.
|| cU || = | c | || U ||.
Y las propiedades de la distancia antes ya mencionadas.
Además cumplen con la desigualdad de Gauchy - Schawarz, desigualdad del triangulo y el teorema de Pitágoras antes yya explicadas.
Proyecciones ortogonales en espacios con producto interno:
Si U y V son vectores en el plano y V es diferente de 0 entonces este se puede proyectar ortogonalmente a U y se denota como
ProyV U = [ ( U%V ) / ( V%V ) ]V
proyU V = [ ( U%V ) / ( U%U ) ]U donde U%V y V%V son el producto punto o producto interno Euclidiano.
Para en el espacio la proyección se denota como proyv U = [ / ]V , proyv U = [ / ]U.
La proyección ortogonal y distancia:
Siendo U y V dos vectores en el espacio V con producto interno y V " 0. Entonces la distancia d ( U, proyv ) < d ( U, cV ) donde c " / .
Definición de conjuntos ortonormales y conjuntos ortogonales:
En un conjunto de vectores S de el espacio vectorial V es producto interno es ortogonal si cada vector de y seria espacio ortonormal si cada vector S es unitario.
Es ortonormal si < vi, vj > = 0 i " j y || vj || = 1 donde i = 1, 2, 3, ..., n y es ortonormal si < vi, vj > = 0 i " j donde vi, vj pertenecen al conjunto s = { v1, v2, ..., vn }
Un conjunto ortogonal es linealmente independiente si s es un conjunto de vectores diferentes de cero y que pertenecen al espacio v con producto interno.
Proceso para ortonormalizar de Gram - Schmidt:
Ver si la base tiene producto interno (como ya lo vimos).
Convertir la base a una base ortogonal.
Sea B = { v1, v2, ..., vn }
w1 = v1
w2 = v2 - proyw1 v2
wn = vn - proyw1 v3 - … - proyw(n-1) vn
B' = { w1, w2, ..., wn }
y para ortonormalizar ui = wi / ||wi|| donde I = 1, 2, ..., n.
Donde B'' = { u1, u2, ..., un } es un abase ortonormal.
Aplicación de los espacios con producto interno:
Producto cruz de dos vectores en el espacio:
Donde U = (u1, u2, ..., un )
V = (v1, v2, ..., vn )
U x V =
por el método de cofactores = i + j + k .
las propiedades del producto cruz:
U x V = V x U
c ( U x V ) = c U x V = U x c V
U x U = 0
U x ( V + W ) = ( U x V ) + ( U x W )
U x 0 = 0 x U
U ( V x W ) = ( U x V ) W
U x V son paralelos si U x V = 0.
Aproximación por mínimos cuadrados:
Siendo f y g dos funciones en x y funciones continuas en un intervalo finito [ a, b ] entonces.
I = 2 dx siendo I = 0 si ( f - g ) ! 0 esto se puede representar como :
= 2 dx siendo I = 2 dx = = || f - g || 2 esto significa que es equivalente minimizar || f - g || 2 y || f - g ||.
La aproximación de minimos cuadrados esta dada por:
g = w1 +w2 + ... + wn siendo w1 = w1 donde b = {w1, w2, w3,}
Combinacion lineal, dependencia e independencia lineal
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por sendos escalares

Cualquier vector se puede poner como combinación lineal de otros que tengan distinta dirección.
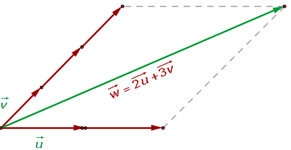

Dados los vectores
calcular el vector combinación lineal

(2,1) = a(3,-2)+(1,4)
(2,1)= (3a,-2a)+ (b,4b)
(2,1)= (3a+b,-2a+4b)
2 = 3a + b
1 = -2a + 4b
a = 1/2
b = 1/2

____________________________________________________________________________________
Dependencia lineal
Varios vectores libres del plano son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal

Propiedades
1.Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los otros.


Si un vector es combinación lineal de otros, entonces todos los vectores son linealmente dependientes.
2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.
3.Dos vectores del plano U = (u1,u2) y V = (v1,v2)son linealmente dependientes si sus componentes son proporcionales.
Independencia lineal
Varios vectores libres son linealmente independientes si ninguno de ellos se puede expresar como combinación lineal de los otros.
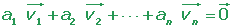
a1 = a2 = ... = 0
Los vectores linealmente independientes tienen distinta dirección
EJERCICIOS:
*Estudiar la dependencia lineal de los vectores: u = (3,1) y v = (2,3)
3/2 = 1/3 3.3 # 2.1
Son linealmente dependientes
*Estudiar la dependenci lineal de los vectores u = (x - 1, 3) y v = (x + 1, 5)
x-1/3 = x+1/5 5x-5 = 3x+3
x = 4
Son linealmente dependientes para x = 4
*Estudiar la dependencia lineal de los vectores:
u = (5, 3 - x) y v = (x + 9, 3x + 1)
5/x+9 = 3-x/3x+1
15x + 5 = 3x - x^2 + 27 - 9x
x = 1
x = -22
Son linealmente dependientes para x = 1 y x = -22

Cualquier vector se puede poner como combinación lineal de otros que tengan distinta dirección.


Dados los vectores

calcular el vector combinación lineal


(2,1) = a(3,-2)+(1,4)
(2,1)= (3a,-2a)+ (b,4b)
(2,1)= (3a+b,-2a+4b)
2 = 3a + b
1 = -2a + 4b
a = 1/2
b = 1/2

____________________________________________________________________________________
Dependencia lineal
Varios vectores libres del plano son linealmente dependientes si existe una combinación lineal de ellos que sea igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal

Propiedades
1.Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los otros.


Si un vector es combinación lineal de otros, entonces todos los vectores son linealmente dependientes.
2.Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos.
3.Dos vectores del plano U = (u1,u2) y V = (v1,v2)son linealmente dependientes si sus componentes son proporcionales.
Independencia lineal
Varios vectores libres son linealmente independientes si ninguno de ellos se puede expresar como combinación lineal de los otros.
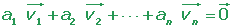
a1 = a2 = ... = 0
Los vectores linealmente independientes tienen distinta dirección
EJERCICIOS:
*Estudiar la dependencia lineal de los vectores: u = (3,1) y v = (2,3)
3/2 = 1/3 3.3 # 2.1
Son linealmente dependientes
*Estudiar la dependenci lineal de los vectores u = (x - 1, 3) y v = (x + 1, 5)
x-1/3 = x+1/5 5x-5 = 3x+3
x = 4
Son linealmente dependientes para x = 4
*Estudiar la dependencia lineal de los vectores:
u = (5, 3 - x) y v = (x + 9, 3x + 1)
5/x+9 = 3-x/3x+1
15x + 5 = 3x - x^2 + 27 - 9x
x = 1
x = -22
Son linealmente dependientes para x = 1 y x = -22
jueves, 25 de marzo de 2010
UNIDAD 4 ESPACIOS VECTORIALES
Un espacio vectorial es aquel conjunto de vectores que cumple las propiedades o axiomas de la suma de vectores y la multiplicación por un escalar dichas propiedades vistas en espacios n-dimensiónales Rn o R2. Un espacio vectorial es un espacio no vacío.
En el estudio de las matemáticas o de la física, el término vector se aplica a una amplia variedad de objetos, principalmente a cantidades que representan magnitudes y dirección ya sea un fuerza, una velocidad o una distancia. El término vector también se usa para describir entidades como matrices, polinomios o funciones.
Podríamos decir que un espacio vectorial es la abstracción de las propiedades de un espacio n-dimencional , debe tomarse en cuenta que en el espacio vectorial no se especifica operaciones ni vectores entonces se puede usar cualquier vector y cualquier operación se puede sustituir la suma de vectores y la multiplicación por un escalar, pero siempre cumpliendo todos las propiedades, siempre seria un espacio vectorial.
Un espacio vectorial cumple con cuatro partes que son: un conjunto de vectores, un conjunto de escalares, y dos operaciones. Estos forman un cuerpo que es igual a las estructuras algebraicas de dos operaciones (un cuerpo). Para comprobar que determinado conjunto es un espacio vectorial es preciso definir o especificar las propiedades de suma multiplicación por un escalar como vimos anteriormente tenemos que definir el elemento que actúa como cero (0) y el negado de cada elemento.
A continuacion una definicion mas formal de lo que es un espacio vectorial
Sea V un conjunto en el cual dos operaciones, llamadas adicion y multiplicacion escalar, han sido definidas. Si u y v se encuentran en V, la suma de u y v se denota por medio de u + v y si c es un escalar, el multiplo escalar de u por c se denota como cu. Si los siguientes axiomas son validos para todo u, v y w en V y para todos los escalares c y d, entonces V se denomina espacio vectorial y sus elementos son llamados vectores.
1. u + v está en V. Cerradura bajo la adición
2. u + v = v + u. Conmutabilidad
3. u +(v + w)=(u + v)+ w. Asociatividad
4. Existe un elemento 0 en V, denominado vector cero o nulo, tal que u + 0 = u.
5. Para cada u en V, existe un elemento -u en V tal que u + (-u)= 0
6. cu esta en V. Cerradura bajo la multiplicacion escalar.
7. c(u + v)= cu + cv. Distributividad
8. (c + d)u = cu + du. Distributividad
9. c(du) = (cd)u. Asociatividad.
10. 1(u)= u. Identidad escalar
A continuacion algunos videos de la definicion de un espacio vectorial y sus propiedades
En el estudio de las matemáticas o de la física, el término vector se aplica a una amplia variedad de objetos, principalmente a cantidades que representan magnitudes y dirección ya sea un fuerza, una velocidad o una distancia. El término vector también se usa para describir entidades como matrices, polinomios o funciones.
Podríamos decir que un espacio vectorial es la abstracción de las propiedades de un espacio n-dimencional , debe tomarse en cuenta que en el espacio vectorial no se especifica operaciones ni vectores entonces se puede usar cualquier vector y cualquier operación se puede sustituir la suma de vectores y la multiplicación por un escalar, pero siempre cumpliendo todos las propiedades, siempre seria un espacio vectorial.
Un espacio vectorial cumple con cuatro partes que son: un conjunto de vectores, un conjunto de escalares, y dos operaciones. Estos forman un cuerpo que es igual a las estructuras algebraicas de dos operaciones
A continuacion una definicion mas formal de lo que es un espacio vectorial
Sea V un conjunto en el cual dos operaciones, llamadas adicion y multiplicacion escalar, han sido definidas. Si u y v se encuentran en V, la suma de u y v se denota por medio de u + v y si c es un escalar, el multiplo escalar de u por c se denota como cu. Si los siguientes axiomas son validos para todo u, v y w en V y para todos los escalares c y d, entonces V se denomina espacio vectorial y sus elementos son llamados vectores.
1. u + v está en V. Cerradura bajo la adición
2. u + v = v + u. Conmutabilidad
3. u +(v + w)=(u + v)+ w. Asociatividad
4. Existe un elemento 0 en V, denominado vector cero o nulo, tal que u + 0 = u.
5. Para cada u en V, existe un elemento -u en V tal que u + (-u)= 0
6. cu esta en V. Cerradura bajo la multiplicacion escalar.
7. c(u + v)= cu + cv. Distributividad
8. (c + d)u = cu + du. Distributividad
9. c(du) = (cd)u. Asociatividad.
10. 1(u)= u. Identidad escalar
A continuacion algunos videos de la definicion de un espacio vectorial y sus propiedades
martes, 2 de marzo de 2010
ELIMINACION DE GAUSS-JORDAN
Camile Jordan:Pionero de la teoría de las matrices, es famoso por el teorema de las curvas de Jordán, el cual afirma que una curva cerrada simple (tal como la circunferencia) "divide al plano en dos regiones conexas agenas"
X1 + 3X2 + 2X3 +2X5 = 0
2X1 + 6X2 - 5X3 - 2X4 + 4X5 - 3X6=-1
5X3 + 10X4 + 15x6=5
2X1 + 6X2 + 8X4 + 4X5 +18X6=6
La matriz aumentada del sistema es
1 3 -2 0 2 0 0
2 6 -5 -2 4 -3 -1
0 0 5 10 0 15 5
2 6 0 8 4 18 6
Sumando el primer renglón multiplicado por -2 al segundo y cuarto renglón se obtienen
1 3 -2 0 2 0 0
0 0 -1 -2 0 -3 -1
0 0 5 10 0 15 5
0 0 4 8 0 18 6
Multiplicad el renglón dos por -1 y después sumando el segundo renglón por -5 al tercero y al segundo renglón multiplicador -4, al cuarto se obtiene
1 3 -2 0 2 0 0
0 0 1 2 0 0 1
0 0 0 0 0 0 0
0 0 0 0 0 2 2
Intercambiando el tercer y cuarto renglón y después multiplicando el tercer renglón de la matriz resultante por un sexto se obtiene la forma escalonada
1 3 -2 0 2 0 0
0 0 1 2 0 3 0
0 0 0 0 0 1 1/3
0 0 0 0 0 0 0
Sumando el tercer renglón multiplicado por -3 al segundo renglon y después sumando el segundo renglon de la matriz resultante multiplicado por dos al primero se obtiene la forma escalonada reducida
1 3 0 4 2 0 0
0 0 1 2 0 0 0
0 0 0 0 0 1 1/3
0 0 0 0 0 0 0
El sistema de ecuaciones correspondiente es
X1 + 3X2 + +4X4 + 5X5 =0
X3 +2X4 =0
X6=1/3
Se elimino la ultima ecuación dado que las soluciones de las ecuaciones restantes las satisfacen automanticamente
Despejando las variables principales se obtienen
X1 =-3X2 - 4X4 - 2X5
X3=-2X4
X6=-1/3
Si a X2, X4 y X5 se les asignan los valores arbitrarios R, S y T, respectivamente en conjunto de soluciones queda defino por la forma
X1=-3R - 4S - 2T
X2=R
X3=-2S
X4=S
X5=T
X6=1/3
A menudo es mas conveniente resolver un sistema de ecuaciones lineales llevando la matriz aumentada a la forma escalonada e vez de seguir adelante hasta tener la forma escalonada reducida. Cuando se aplica este ultimo método el sistema por ecuación correspondiente se puede resolver mediante una técnica conocida como sustitucion en reversa.
X1 + 3X2 + 2X3 +2X5 = 0
2X1 + 6X2 - 5X3 - 2X4 + 4X5 - 3X6=-1
5X3 + 10X4 + 15x6=5
2X1 + 6X2 + 8X4 + 4X5 +18X6=6
La matriz aumentada del sistema es
1 3 -2 0 2 0 0
2 6 -5 -2 4 -3 -1
0 0 5 10 0 15 5
2 6 0 8 4 18 6
Sumando el primer renglón multiplicado por -2 al segundo y cuarto renglón se obtienen
1 3 -2 0 2 0 0
0 0 -1 -2 0 -3 -1
0 0 5 10 0 15 5
0 0 4 8 0 18 6
Multiplicad el renglón dos por -1 y después sumando el segundo renglón por -5 al tercero y al segundo renglón multiplicador -4, al cuarto se obtiene
1 3 -2 0 2 0 0
0 0 1 2 0 0 1
0 0 0 0 0 0 0
0 0 0 0 0 2 2
Intercambiando el tercer y cuarto renglón y después multiplicando el tercer renglón de la matriz resultante por un sexto se obtiene la forma escalonada
1 3 -2 0 2 0 0
0 0 1 2 0 3 0
0 0 0 0 0 1 1/3
0 0 0 0 0 0 0
Sumando el tercer renglón multiplicado por -3 al segundo renglon y después sumando el segundo renglon de la matriz resultante multiplicado por dos al primero se obtiene la forma escalonada reducida
1 3 0 4 2 0 0
0 0 1 2 0 0 0
0 0 0 0 0 1 1/3
0 0 0 0 0 0 0
El sistema de ecuaciones correspondiente es
X1 + 3X2 + +4X4 + 5X5 =0
X3 +2X4 =0
X6=1/3
Se elimino la ultima ecuación dado que las soluciones de las ecuaciones restantes las satisfacen automanticamente
Despejando las variables principales se obtienen
X1 =-3X2 - 4X4 - 2X5
X3=-2X4
X6=-1/3
Si a X2, X4 y X5 se les asignan los valores arbitrarios R, S y T, respectivamente en conjunto de soluciones queda defino por la forma
X1=-3R - 4S - 2T
X2=R
X3=-2S
X4=S
X5=T
X6=1/3
A menudo es mas conveniente resolver un sistema de ecuaciones lineales llevando la matriz aumentada a la forma escalonada e vez de seguir adelante hasta tener la forma escalonada reducida. Cuando se aplica este ultimo método el sistema por ecuación correspondiente se puede resolver mediante una técnica conocida como sustitucion en reversa.
Suscribirse a:
Entradas (Atom)

